Introduction
DC to DC converters are used primarily whenever it is necessary to provide specific voltage supplies from a single primary power source and consequently they find wide application in battery powered and mains powered electronic equipment. They operate by converting the primary power source voltage to an alternating voltage suitable for transforming and rectifying to the required operating voltage(s); the voltage transformation being effected by means of capacitance or inductance (transformers and chokes). Of these the latter is by far the most widely used and which is the subject of this note. The conversion of the source voltage to an alternating voltage is achieved by switching/commutating it to a transformer or choke by electronic switches (transistors) in an oscillatory circuit; the transformer or choke being a component of the oscillator or not as the case may be. The input voltage waveform so produced is therefore a square wave. Square wave drive is used in the majority of dc to dc converter circuits, although sine wave converters are used for specific applications.
Fundamentals
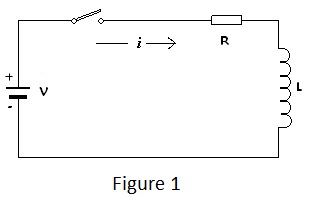
Consider the simple circuit of Figure 1 including an inductance ‘L’ Henrys, inevitable circuit resistance ‘R’ Ohms, a switch and a battery providing a source of electro-motive force (emf) of ‘V’ volts.


|
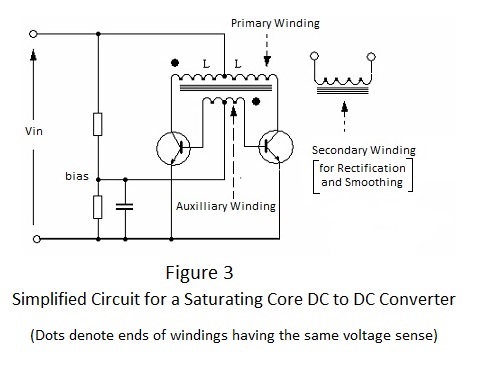 |
In the simplified circuit depicted in Figure 3, the primary inductors constitute a centre tapped winding with the tap connected to the primary power source Vin and the winding ends connected to transistor switches. Accepting that, at any instant, when one switch is on the other is off; the winding connected to the ‘ON’ switch will have Vin applied to it. The total primary winding constitutes an auto transformer and consequently the end connected to the ‘OFF’ switch must be at a potential of 2Vin; a factor to be taken into account when selecting the type of transistor to be used. A coupled winding, also centre tapped, is connected at the tap to a point which produces a low forward bias at the transistor base terminals connected to the ends of the winding. The turns on this auxiliary winding are such that each half generates a volt or so and the sense of its connection is such that the voltage generated enhances the forward bias for an ‘ON’ transistor switch and opposes the bias applied to its companion; holding the latter in the ’OFF’ state. From the instant a transistor is switched on, its collector current rises linearly until the onset of core saturation, as shown in Figure 2B. At the onset of saturation the current starts to rise steeply but the coupling between the primary winding and the auxiliary winding weakens due to the effective loss of a ferromagnetic core to concentrate the magnetic flux linking them. Thus the base drive voltage for the ‘ON’ transistor becomes insufficient to maintain its collector current –let alone increase it – and the reverse voltage at the base of the ‘OFF’ transistor becomes insufficient to prevent it from conducting. The action of falling conduction for one transistor and rising conduction for the other is cumulative; resulting in a reversal of the on/off status of the transistor switches each time saturation current is reached. Thus an alternating square wave voltage of amplitude 2Vin is applied to the primary winding. The half period of this waveform is the time for the current in each half primary to reach the level for core saturation and, as this period varies inversely with Vin, the running frequency is proportional to Vin. |
 |
| This winding has work to do, i.e. it has not only to generate a voltage but it also has to supply current to a load. Now transformer theory decrees that, if the secondary of a transformer supplies current, an equivalent current – given by the product of the secondary current and the inverse of the turns ratio – must be drawn from the input supply by the primary winding and, by virtue of the fact that the drive waveform is a square wave, this current is of square wave form. Thus the current flowing in one half of the primary takes the form shown in Figure 4. |
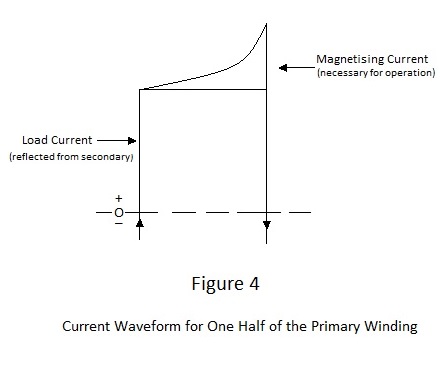 |
From Figure 4 it can be seen that the ramp of magnetising current, necessary to make the transformer work, rides on a much larger ‘block’ of load current. This is a necessary condition for efficiency, as the former plays no plays no part in the transfer of power from primary to secondary. The astute reader might ask why a high load current can flow in the primary winding when, as already has been discussed, it reaches saturation at a relatively small magnetising current. The answer to this is that the effect of load current in the secondary winding is to demagnetise the core and it is therefore necessary for the primary winding to draw the appropriate current to maintain magnetisation. Thus primary load Ampère-turns cancel secondary Ampère-turns such the net Ampère-turns applied to the core remains unchanged from that for the unloaded condition. |
Other push–pull Converter circuits |
|
 |
All of the following circuits are shown in their simplest form and for optimum performance additional components might be required. These additional components usually minimise the effects of the non-ideal performance of the transistor switches. Also the circuits do not address rectification, stabilisation and regulation and they show only a single secondary winding. There is no reason why the circuits are limited to the generation of a single voltage supply and further supplies can be provided by additional secondary windings. With regard to stabilisation and regulation, it is customary for the input voltage Vin. to be the output of a linear voltage regulator, particularly when a number of secondary supplies are required. This is quite satisfactory when the secondary loads are fixed because the converter source impedance is relatively low, but efficiency can be poor if the circuit is required to operate with a wide variation of the primary power source voltage; particularly when the latter is at the high end of its range. Secondary supplies can of course be regulated but this is obviously not cost effective when multiple supplies are required. |
| Figure 5 shows the simplest type of push-pull converter circuit. It has no auxiliary feedback winding to provide the appropriately sensed drive to the base terminals of the transistor switches, the base drive for an ‘ON’ switch being obtained by resistance coupling from 2Vin. potential at the collector of its ‘OFF’ counterpart. Pre-saturation switching can be effected by arranging this cross coupling to limit the base drive and consequently the available collector current of the switch transistors. This, however, is not really practical due to the wide variation of the HFE. parameter for transistors of a given type and restricting collector current to that required for operation obviates any capability for the supply of significant load current. Therefore the output impedance tends to be high and the running frequency to be load dependent if switching is not controlled by core saturation. | |
It must be concluded therefore that core saturation is still the dominant factor determining the switching periods for practical applications. Despite these shortcomings, this type of circuit has been used extensively because of its simplicity and avoidance of the need to take account of the sense of windings in its operation. |
|
The circuit of Figure 6 imposes strict control of the switch ‘ON’ periods which can be set to preclude the magnetising current from reaching saturation. It employs an untapped and ‘floating’ feedback winding to generate the essential base drive current. However, in this case the winding is coupled to the transistor base terminals via series resistance and capacitance. The effect of this arrangement is to cause an initially high level of base drive current to taper off during the ‘ON’ period as the capacitor charges; the period being effectively controlled by the time constant produced by capacitor C and one or other of the two resistors R. The other resistor shown in the circuit, which is of much greater value than R, is necessary to ensure starting.
Correct sensing of the feedback winding relative to the primary is essential and the polarity of the voltage generated reverses for alternative half cycles of the switching waveform. Correctly used, the circuit operates free from the transient effects of core saturation and the effect of one aspect of imperfect transistor switching (delayed switch-off due to minority carrier storage) is reduced by the progressively falling base drive but correspondingly the output impedance is relatively high.
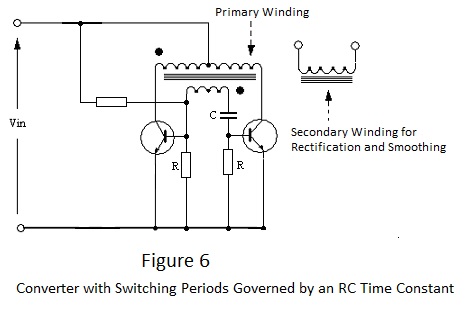 |
The circuit shown in Figure 7 is the author’s favourite type of push-pull converter as it overcomes most of the problems discussed or mentioned in the foregoing. It utilises MOSFET switches in lieu of bipolar transistors, a method which became practical for power converters with the advent of vertical gate technology. Mosfet switches have two distinct advantages over bipolar transistors: being majority carrier only devices, there is no problem of delayed switch-off and secondly they are voltage driven which obviates the need to supply significant current and consequently enables them to be driven efficiently by the Q and not Q outputs of a separate CMOS astable oscillator, as shown in Figure 7. There is of course no need for an auxiliary feedback winding and the component count is low. |
 |
Switched Mode Converters |
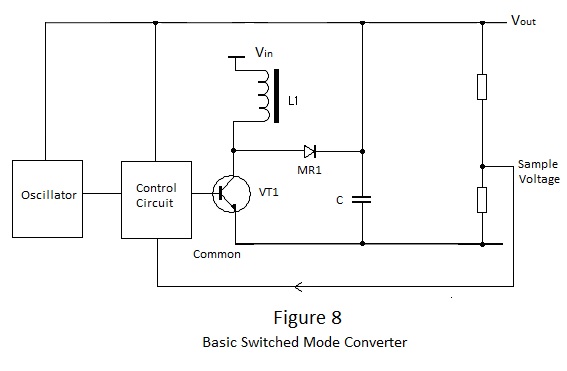 |
In this arrangement a variable voltage generated by L1, is added to the variable primary supply voltage Vin to provide a stable voltage Vout at a given power Pout. The arrangement shown in Figure 8 is not sacrosanct and other configurations are often employed, eg. the voltage generated by L1 may be subtracted from Vin to produce a step down converter or it may be referred to common to make it the actual output voltage. Also, using L1 as a primary, coupled windings may be added to produce additional supplies; their individual power outputs being included in the total Pout. |
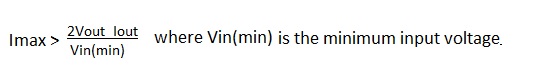 |
And, from the foregoing discussion the value of L1 depends on the value of Imax. Also, assuming that Pout is fixed, the running frequency must be maximum at Vin (min) and it cannot exceed the reciprocal of the transfer cycle period; upon which the value of L1 is also dependent. To extract ourselves from such a conundrum it is necessary to impose constraints: |
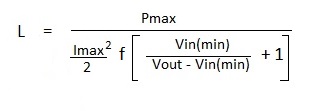 |
For the power levels and constraints involved in a typical portable instrument application, the value of L1 for a 20kHz converter falls in the range 100μH to 200μH a value which could conveniently be wound air cored. However to minimise resistance and electromagnetic radiation the coil must be wound on a gapped magnetic core. |
Sine –Wave Converters |
|||
 |