A Simplified study of the Atom and Radioactivity
The atom comprises a nucleus of ≈ 10 exp-12cm diameter, around which electrons orbit in defined radial regions (often called shells) out to a diameter of ≈ 10 exp-8cm; somewhat akin to orbiting planets in the solar system. The atom contains thus, something like 10 exp 12 times more free space than matter. (atomic radius ≈ 1.5 x 10 exp-13 x A exp 0.33cm, where A is the atomic mass).
The tightly packed nucleus contains roughly equal numbers of two types of particle. These have different but closely similar mass approximating to one atomic mass unit (amu) which equals 1.6477 x 10 exp-24 grams which is nearly 2000 times the mass of an electron.
One of these particles (the Proton) has a mass of 1,008142 amu. and unit positive charge; i.e. equal to but opposite to that of an electron (1.602 x 10 exp-19 Coulombs).
The other (the Neutron) has a mass of 1.008982 amu. It possesses no charge.
The nucleus of ‘normal’ hydrogen has one proton and no neutrons and thus the proton is symbolised . Similarly, a neutron is symbolised . Similarly, a neutron is symbolised 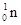 . The significance of the superscript and subscript numbers can best be illustrated by an example - . The significance of the superscript and subscript numbers can best be illustrated by an example -
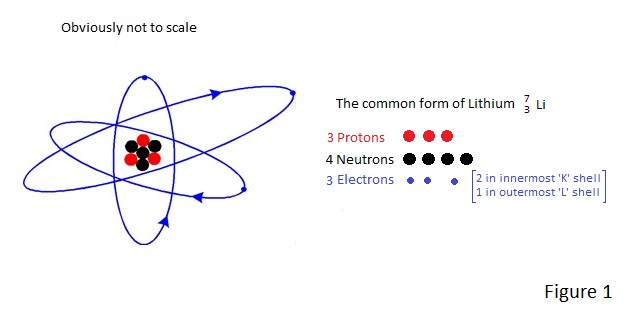
Take the element Lithium which may be depicted as shown in Figure 1. |
From this example, it is clear that the superscript number denotes the number of nucleons (protons plus neutrons) in a nucleus. It is called the Atomic Mass and is symbolised ‘A’.
It is also clear that the subscript figure denotes the number of protons in a nucleus. It is called the Atomic Number and is symbolised ‘Z’.
Z is what determines what an element is and A determined which isotope (Nuclide) we are concerned with; e.g. the Figure 1 example depicts the most common isotope of Lithium –Lithium 7.
Lithium can also exist with 3 neutrons in the nucleus as the isotope Lithium 6.
Digressing slightly; the number of electrons orbiting the nucleus is equal to Z and the number of these in the outermost shell determines how an element behaves chemically. Although not included in isotopic symbolisation, we frequently need to refer to the number of neutrons by the Neutron Number ‘N’.
Obviously N = A – Z
It is probably worthwhile to consider why the atom exists in this form:
Consider first the nucleus – like charges repel so there must be electrostatic (Coulomb) force tending to blow the protons out of the nucleus. It might be argued that, as nucleons have mass, gravitational attraction will overcome Coulomb repulsion. However calculation demonstrates that the gravitational force between adjacent protons is minute compared with the electrostatic force and that the additional gravitational force, and dilution of the electrostatic force due to the presence of neutrons, is of little consequence. Therefore some other influence must be involved if the nucleus is not to disintegrate.
A number of dynamic attractive influences are beyond the scope of this simple study but the major influence is that of Mass Deficit. Mass Deficit is the phenomenon that the total mass of the nucleus is less than the sum of its parts.
Take for instance our Lithium 7 atom.
Total mass of protons =3 x 1.008142 amu.
Total mass of neutrons =4 X1.008982 amu.
Total theoretical mass = 7.060354 amu.
Actual Mass of Lithium 7 neucleus = 7.018200 amu.
Mass Deficit = 0.044154 amu
| |
How does this peculiar loss of mass result in a force which is strong enough to hold the nucleus together?
To understand this we need to employ the expression which emanates from Einstein’s special theory of relativity: |
|
A formula with which most people are familiar but of which relatively few understand the significance.
Einstein’s simple formula defines the equivalence of energy and mass and that consequently mass may be transmuted to energy and vice versa.
From this it follows that a mass deficit may be equated to a loss of energy which may be considered to be negative energy because it acts to hold the nucleus together.
This energy is called the Binding Energy and, because Energy = Force x Distance, it results in a binding force within its sphere of influence.
What is the binding energy due to the Lithium 7 defect?
Putting 1 amu into Einstein’s formula yields: 1 amu = 931 MeV (Million electron-volts)
or 1.4896 x 10exp -10 Joules
The mass defect is thus equivalent to 0.044154 x 931 = 41.1 MeV
41.1 MeV is the total binding energy for the Lithium 7 nucleus: what is more relevant to nuclear stability is the mean binding energy per nucleon 41.1 / 7 ≈ 5.86 MeV
The binding energy per nucleon is a measure of the packing density of nucleons within the nucleus. It varies from element to element, isotope to isotope and with atomic mass as depicted in Figure 2. |
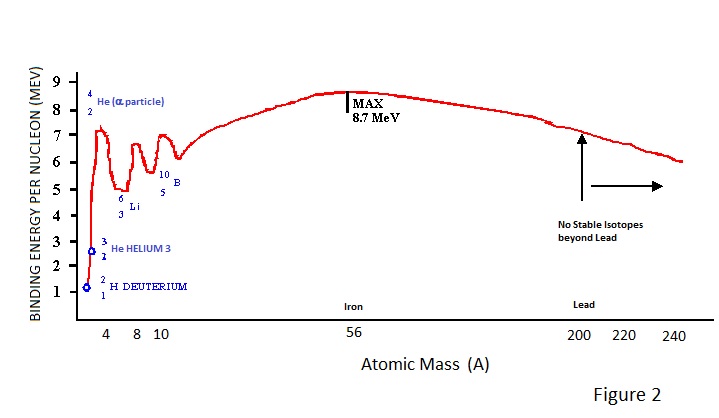 |
From Figure 2 it can be seen that binding energy initially rises rapidly with increasing atomic mass, and then more gradually to reach a maximum value of 8.7MeV at an atomic mass of about 56 (iron) and above which it falls relatively slowly. It can also be seen that this general trend is subject to marked peaks and troughs for the light elements; an example of this being the relatively high binding energy for Helium. The Helium 4 nucleus of 2 Protons + 2 Neutrons constitutes an alpha particle (α) and its inherent stability probably explains why heavy unstable nuclides (atomic mass > lead) can decay by the emission of α particles. |
Clearly, if binding energy due to the mass defect is of paramount importance, most nuclei would be expected to be stable and to have no radioactive isotopes (nuclides). In fact, nearly all elements have radioactive isotopes and that therefore imbalance between the number of protons and neutrons in a nucleus must play a part in determining its stability.
A detailed explanation of why proton – neutron imbalance influences the stability of a nucleus is outside the scope of this simple study but forces known as exchange forces are involved. Apparently neutrons and protons spontaneously interchange identities and imbalance effectively modulates the force element of binding energy.
Additionally the spatial presence of neutrons within a nucleus must dilute the Coulomb repulsion between protons and for this reason nuclei having excess neutrons would be expected to be more stable than ones having a neutron deficit.
This is in fact the case and thus, with increasing mass number, stable nuclides have a surfeit of neutrons. However for elements of greater mass number than that of lead binding energy reduces due to the proportionally reduced significance of mass deficit; resulting in a different form of nuclear instability.
Nuclear stability and instability is best illustrated by a plot of Z versus N for elements and their isotopes as shown in Figure 3 which is the basis of the ‘Chart of the Nuclides’ which adorns many an office wall in nuclear establishments. |
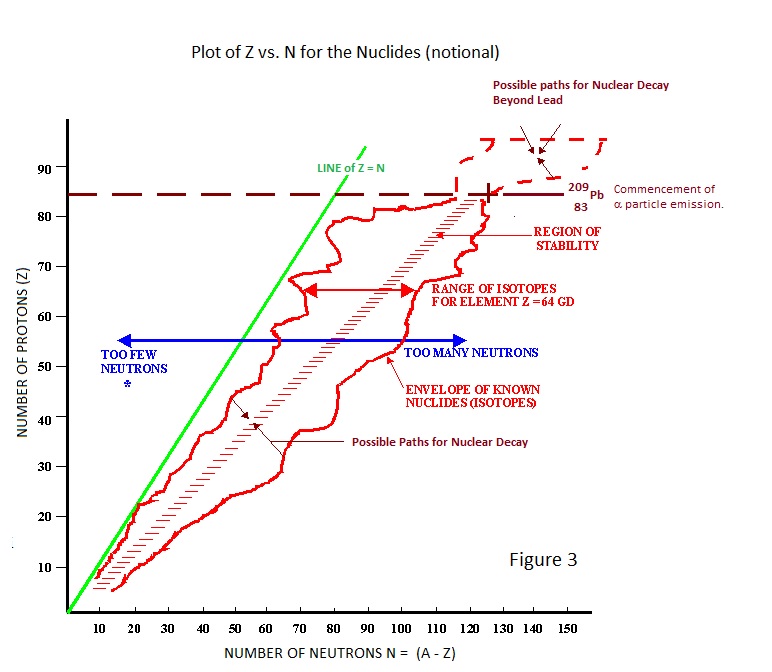 |
The figure epitomises the foregoing discussion and leads to discussion of the various ways nuclei ‘decay’ to a stable state.
* Most graphical representations of nuclear stability/instability label the area to the left and above the region of stability as having excess protons. A convention which aids discussion of the paths by which nuclides attain stability but which is illogical because it is Z – the proton number- which identifies an element and its isotopes. However we will follow the convention in the interest of compatibility and ease of discussion. |
How do Unstable Nuclei decay to become Stable Nuclei?
Discussion is probably best served by listing the facts with or without explanation and to develop them where possible.
1. Nuclei with excess protons (insufficient neutrons) do not decay by emitting protons
2. Nuclei with excess neutrons do not decay by emitting neutrons
3. Nuclei which are too massive to be stable (mass numbers greater than lead) do not split asunder (fission) but decay primarily by emitting particles of mass 4 (2P + 2N) = Helium nucleus = α particle.
4. In the course of decaying to lead by successive a particle decay, massive nuclei also decay to correct proton-neutron imbalance.
5. Dependent upon the degree of proton-neutron imbalance a number of decay steps (up to seven) might be involved in the path from unstable nucleus to stable nucleus.
6. Following a decay step a nucleus is usually left in a temporarily excited state. Equilibrium is normally achieved by the emission of a packet of electromagnetic radiation i.e. a gamma photon.
7. Decay occurs at random characteristically taking from fractions of a second to thousands of years. The time for half of the atoms of a parent nuclide to decay is called the Half Life. |
Development of the above.
1. A nucleus with a proton excess decays to produce a new nucleus (and hence element) by having Z reduced by one, N increased by one with A of course remaining essentially unchanged. This occurs by one of two ways:
A) Electron Capture - By which a proton transmutes to a neutron by capturing an orbiting electron; this capture often being accompanied by electromagnetic radiation resulting from de-excitation of the nucleus (gamma) and always resulting from the de-excitation of the atom by re-establishment of the system of electron orbits (X-ray).
An example of a nuclide which decays by electron capture is Iron 55 which decays to Manganese 55. In this case the nucleus is not left in an excited state so a gamma (γ) photon is not emitted. However re-establishment of the equilibrium of the orbiting electrons results in the emission of a 6 keV x-ray.
Iron 55 is used as an energy reference for the calibration of x-ray counters and for counters used in tritium monitoring. Its half- life is 2.6 years.
B) Positron Emission - By which a proton transmutes to a neutron by the emission of a positively charged particle otherwise identical to an electron. The emission usually being accompanied by the emission of a gamma photon as the nucleus returns to equilibrium (its ground state). This positively charged particle (positron) is an example of anti-matter, so beloved of science fiction writers. It cannot exist in the atomic system of our universe and it rapidly co-annihilates with the first electron it encounters; resulting in two 511 keV photons which travel in opposite directions. This is another example of the transmutation of matter into energy in accordance with Einstein's famous formula.
Sodium 22 is an example of a nuclide which decays by positron emission to Neon 22. The positron is emitted with 540 keV kinetic energy accompanied by a 1.28 MeV γ photon as the nucleus returns to ground state.
Sodium 22is used as a reference source for the calibration of γ spectrometers. Present in a spectrum are 1.28 MeV γ photons, 511 keV annihilation photons and a 1.791 MeV response due to their coincident sum energy,
It is interesting to note that Sodium 22 is an unstable isotope with equal numbers of protons and neutrons. It is an example of the previously discussed finding that the condition for stability is biased towards neutron excess.
The half-life of Sodium 22 is 2.58 years.
2. An unstable nucleus with neutron excess decays to produce a new nucleus (and hence element) having Z increased by 1, N reduced by 1 with A of course remaining unchanged. This occurs by one way only:-
β Particle Emission – By which a neutron transmutes to a proton by emitting a negatively charged particle which is identical with an electron but known as a beta particle because of its nuclear origin.
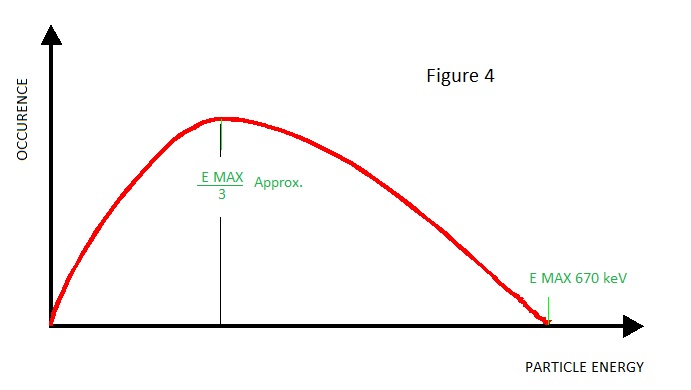
As with any nuclear transmutation there is a possibility of γ emission due to de-excitation. Logically, because there is only one decay mode, β particle emission might be expected to be straightforward but strangely β particles are emitted with varying kinetic energy from 'zero'up to a maximum of E max.
If we observe the occurrence vs. energy of the beta particles from Krypton 85, we obtain a plot as shown in Figure 4.
|
|
At first sight this phenomenon contravenes the law of energy conservation – it should not happen because particles of energy less than E max have lost energy and energy cannot be lost, only converted.
Scientists puzzled over this conundrum for quite a time before an acceptable theory emerged. It was concluded that the missing energy is in fact imparted to an uncharged particle of probably less than electron mass - i.e. one 2 thousanth of an amu. - the Neutrino.
Being small and non-ionising, the neutrino is extremely penetrating and virtually impossible to detect!
3. Massive (beyond lead) nuclei decay primarily by alpha (α) particle emission, whereby A is reduced by four . Probably this stems from the fact that the helium nucleus is the smallest assembly of protons and neutrons with high binding force and is therefore very stable. However among the transuranic elements there are rare instances of isotopes which fission spontaneously and in consequence emit neutrons as well as fission fragments. An example of a nuclide which fissions spontaneously is Plutonium 240. |
Electrons
Electrons, equal in number to Z, orbit the nucleus in clearly defined regions or shells. These shells are by convention labelled ‘K’, ‘L’, ‘M’ etc. with the K shell innermost. The shells correspond to quantum energy levels which are inter-related by whole numbers; i.e. their quantum energy number ‘n’.
‘n’ can only be a whole number 1, 2, 3 etc. According to quantum theory there can be no intermediate levels. Thus electrons in the K shell are at quantum level 1 and those in the L shell are at quantum level 2 etc.
Within the quantum shells, individual electrons have slightly varied energy levels due to spin and other parameters outside of this study.
With all of the electrons in their ‘proper places’ an atom is said to be in the Ground State but with any electron out of place the atom is in excited state. If an electron is missing from the outermost shell or an additional electron is present the atom is an ion.
Clearly the energy necessary to remove an electron from an inner shell is greater than that necessary to remove one from an outer shell. The energy required to remove inner electrons also depends upon the size of the atom (actually its Z number).
As a rough approximation the energy required to remove a K shell electron varies with Z to the fifth power and thus only 13 eV or so are required to remove the singe K shell electron from an hydrogen atom, where as something like 100 keV is required to displace a K shell electron from uranium. Correspondingly photons (x-rays) of similar but slightly lower energy are emitted when the excited atom restores equilibrium.
The number of electrons occupying a shell is governed by the Pauli Exclusion Principle and is given by the expression 2 x n squared where n is the quantum number as mentioned in the foregoing.
Therefore only two electrons can occupy the K shell of any atom, 8 in the L shell, 18 in the M shell, 32 in the N shell and 50 in the P shell. Only the outermost shell of an atom can be unfilled and the deficit determines how an atom (element) behaves chemically with other elements. Any atom (element) having a full outer shell is chemically inert as typified by the inert gases helium and neon. |
Thank you for reading.
|
All content is free to use.
|
![]() . Similarly, a neutron is symbolised
. Similarly, a neutron is symbolised ![]() . The significance of the superscript and subscript numbers can best be illustrated by an example -
. The significance of the superscript and subscript numbers can best be illustrated by an example -